Viens solis! Antenas visu veidu aprēķinu formulas kopsavilkums
Aptuvenais 8 minūtes, lai pabeigtu lasīšanu
Pēc dažādu svarīgo antenu parametru ieviešanas mēs ieiesim dziļākā apgabalā, kas ir ar parametriem saistītās aprēķina formulas. Katra formula nodrošinās daudz ērtības pirms un pēc uzstādīšanas. Šīs formulas ir apkopotas šajā numurā, ne tikai var atrisināt dažādus jautājumus lietošanas laikā, bet arī sniegt idejas turpmākajam antenas izkārtojumam.
Antenas pastiprinājums ir parametrs, lai izmērītu antenas starojuma virziena kartes virziena pakāpi. Augsta pastiprinājuma antena piešķirs prioritāti noteiktam starojuma signāla virzienam. Antenas pastiprināšana ir pasīva parādība, jaudu nepalielina antena, bet vienkārši pārdala tā, lai nodrošinātu lielāku izstarotās jaudas noteiktā virzienā nekā citas izotropās antenas.
↓ Tālāk ir sniegti daži aptuvenie antenas pastiprinājuma vienādojumi.
Vispārējā antena
G(dBi) = 10 Lg {32000 / (2θ3dB,E × 2θ3dB,H)}
Formulā 2θ3dB,E un 2θ3dB,H ir attiecīgi antenas atloku platums divās galvenajās plaknēs; 32000 ir statistikas empīriskie dati.
Paraboliskā antena
G (dBi) = 10 Lg{4,5 × (D/λ0)2}
Formulā D ir paraboloīda diametrs; λ0 ir centra darba viļņa garums; 4.5 ir statistikas empīriskie dati.
Vertikāla daudzvirzienu antena
G(dBi) = 10 Lg { 2 L / λ0 }
Formulā L ir antenas garums; λ0 ir centra darba viļņa garums.
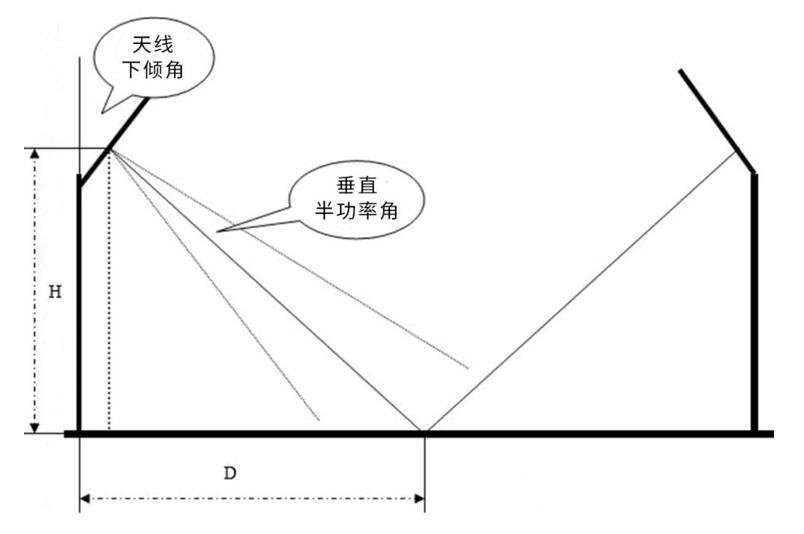
Vissvarīgākais antenas regulēšanā ir precīzi noregulēt tās slīpuma leņķi (kas var atrisināt problēmas ar vāju pārklājumu, pārklājuma pārklājumu utt.). Tālāk ir sniegts ievads tās oriģinālākajā antenas slīpuma leņķa aprēķināšanas metodē.
Antenas aprēķina formula intensīvas satiksmes zonai (pilsētas zonai).
Antenas slīpuma leņķis = Arctag(H/D) + vertikāls pusjaudas leņķis / 2
Zemas apkalpošanas zonas (lauku, piepilsētu uc) antenas formula.
Antenas slīpuma leņķis = loka zīme (H/D)
Parametra apraksts.
(1) antenas slīpuma leņķis: leņķis starp antenu un vertikālo virzienu.
(2) H: antenas augstums. To var izmērīt tieši.
(3) D: šūnu pārklājuma rādiuss. Parasti D vērtību nosaka ceļa testā, lai nodrošinātu pārklājumu faktiskajā projektā, parasti D ir jābūt lielākam, lai nodrošinātu pārklājuma pārklāšanos starp blakus esošajām šūnām.
(4) Vertikālais pusjaudas leņķis: antenas vertikālais pusjaudas leņķis, parasti 10 grādi.
Virzienu diagramma, priekšējā un aizmugurējā atloka maksimālās vērtības attiecību sauc par priekšējo un aizmugurējo attiecību, kas reģistrēta kā F / B . Pirms un pēc nekā lielāka, antena pēc starojuma (vai uztveršanas) ir mazāka. Pirms un pēc F / B attiecību ir ļoti vienkārši aprēķināt:
F / B = 10 Lg {(forward jaudas blīvums) / (atpakaļ jaudas blīvums)}
Parametra apraksts: antenas priekšpuses un aizmugures attiecība F / B, tās tipiskā vērtība ir (18 ~ 30) dB, īpašos apstākļos nepieciešama līdz (35 ~ 40) dB.
Signāla sprieguma un signāla strāvas attiecību antenas ieejā sauc par antenas ieejas pretestību. Ievades pretestībai ir pretestības komponents Rin un pretestības komponents Xin, tas ir.
Zin = Rin + j Xin
Reaktīvā komponenta esamība samazinās antenu no padeves līnijas līdz signāla jaudas ieguvei, tāpēc pretestības komponentam jābūt pēc iespējas tālākam nullei, tas ir, antenas ieejas pretestībai jābūt pēc iespējas tālākai tīrai pretestībai.
Faktiski, pat ja antena ir labi izstrādāta un nodota ekspluatācijā, ieejas pretestība vienmēr satur nelielu pretestības komponenta vērtību. Ievades pretestība un antenas struktūra, izmērs un viļņa garums, pusviļņu simetrisks oscilators ir vissvarīgākā pamata antena.
Tā ieejas pretestība ir Zin = 73,1 + j42,5 (omi).
Kad garums ir saīsināts (3-5)%, pretestības komponentu var novērst, lai antenas ieejas pretestība būtu tīra pretestība, tad ieejas pretestība ir Zin = 73,1 omi (nominālā 75 omi). Stingri sakot, tīri rezistīvā antenas ieejas pretestība ir paredzēta tikai punkta frekvencei. Starp citu, pusviļņa salocītā oscilatora ieejas pretestība ir četras reizes lielāka par pusviļņa simetrisko oscilatoru, tas ir, Zin = 280 omi (nominālā 300 omi).
Sprieguma un strāvas attiecība dažādās vietās bezgalīgi garā pārvades līnijā tiek definēta kā pārvades līnijas raksturīgā pretestība un tiek apzīmēta ar Z. Koaksiālā kabeļa raksturīgās pretestības aprēķināšanas formula ir šāda:
Z. = [60/√εr] × Log ( D/d ) [ohm
Formulā D ir koaksiālā kabeļa ārējā vadītāja vara tīkla iekšējais diametrs; d ir koaksiālā kabeļa serdes ārējais diametrs; εr ir izolācijas vides relatīvā dielektriskā konstante starp vadītājiem. Piezīme: Parasti Z. = 50 omi, ir arī Z. = 75 omi.
No iepriekš minētās formulas ir viegli redzēt, ka barošanas līnijas raksturīgā pretestība ir saistīta tikai ar vadītāja diametru D un d un dielektrisko konstanti εr starp vadītājiem, bet ne ar barošanas līnijas garumu, darbības frekvenci un pievienoto slodzes pretestību. uz padeves līnijas termināli.
Signāla pārraide padevējā, papildus vadītāja pretestības zudumam, ir izolācijas materiāla dielektriskie zudumi. Šie divi zudumi palielinās, palielinoties padevēja garumam un darbības frekvencei. Tāpēc saprātīgam izkārtojumam jābūt pēc iespējas īsākam, lai saīsinātu padeves garumu.
Zaudējuma lielumu uz garuma vienību norāda vājinājuma koeficients β, kura mērvienība ir dB / m (decibels / metrs), kabeļa tehniskajās specifikācijās pārsvarā izmantotā vienība dB / 100m (decibeli / simts metri).
Pieņemsim, ka barošanas ievade padevējam ir P1, jauda no L (m) padeves garuma ir P2, pārraides zudumu TL var izteikt šādi.
TL = 10 × Lg ( P1 / P2 ) ( dB )
Vājināšanās koeficients ir: β = TL / L ( dB / m )
Neatbilstības gadījumā padeves līnijā pastāv gan krītoši, gan atspoguļoti viļņi. Vietā, kur krītošie un atstarotie viļņi atrodas vienā fāzē, sprieguma amplitūdas summējas līdz maksimālajai sprieguma amplitūdai Vmax , veidojot viļņu tīklu; savukārt vietā, kur krītošie un atstarotie viļņi atrodas pretējā fāzē, sprieguma amplitūdas atņem līdz minimālajai sprieguma amplitūdai Vmin , veidojot viļņu mezglu. Citu punktu amplitūdas vērtības atrodas starp viļņa vēderu un viļņa mezglu. Šo sintētisko vilni sauc par stāvošo vilni.
A, atstarotā viļņa sprieguma un krītošā viļņa sprieguma amplitūdas attiecību sauc par atstarošanas koeficientu, kas atzīmēts kā R.
R = atstarotā viļņa amplitūda / krītošā viļņa amplitūda = (ZL - Z0) / (ZL + Z0 )
Otrkārt, viļņa vēdera sprieguma attiecību pret viļņa sekcijas sprieguma amplitūdu sauc par stāvviļņu koeficientu, kas pazīstams arī kā sprieguma stāvviļņu attiecība, kas apzīmēts kā VSWR : VSWR = viļņa vēdera sprieguma amplitūda.
VSWR = Vmax/Vmin = (1 +R)/(1-R)
Jo tuvāk ir termināļa slodzes pretestība ZL un raksturīgā pretestība Z0, jo mazāks ir atstarošanas koeficients R, jo tuvāk VSWR ir 1, un jo labāka atbilstība.


















 5g tīkla antena
5g tīkla antena